Khintchine Exponents and Lyapunov Exponents of Continued

Article contents

• Abstract
• References

Abstract

Assume that x∈[0,1) admits its continued fraction expansion x=[a 1(x),a 2(x),…]. The Khintchine exponent γ(x) of x is defined by 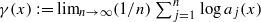when the limit exists. The Khintchine spectrum dim E ξ is studied in detail, where E ξ :={x∈[0,1):γ(x)=ξ}(ξ≥0) and dim denotes the Hausdorff dimension. In particular, we prove the remarkable fact that the Khintchine spectrum dim E ξ , as a function of 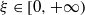, is neither concave nor convex. This is a new phenomenon from the usual point of view of multifractal analysis. Fast Khintchine exponents defined by 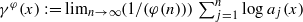are also studied, where φ(n) tends to infinity faster than n does. Under some regular conditions on φ, it is proved that the fast Khintchine spectrum dim ({x∈[0,1]:γ φ(x)=ξ}) is a constant function. Our method also works for other spectra such as the Lyapunov spectrum and the fast Lyapunov spectrum.

Type

Research Article

Copyright

Copyright © 2008 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Barreira, L. , Saussol, B. and Schmeling, J. . Higher-dimensional multifractal analysis. J. Math. Pures Appl. 81 (2002), 67–91.CrossRefGoogle Scholar

[2] Bernstein, F. . Über eine Anwendung der Mengenlehre auf ein der Theorie der säkularen Störungen herrührendes Problem. Math. Ann. 71 (1912), 417–439.CrossRefGoogle Scholar

[3] Billingsley, P. . Ergodic Theory and Information. John Wiley & Sons, New York, 1965.Google Scholar

[4] Borel, E. . Les probabilités dénombrables et leurs applications arithmétiques. Rend. Circ. Mat. Palermo 27 (1909), 247–271.CrossRefGoogle Scholar

[5] Borel, E. . Sur un problème de probabilités relatif aux fractions continues. Math. Ann. 72 (1912), 578–584.CrossRefGoogle Scholar

[7] Brin, M. and Katok, A. . On local entropy. Geometric Dynamics (Lecture Notes in Mathematics, 1007). Springer, Berlin, 1983, pp.30–38.CrossRefGoogle Scholar

[8] Bumby, R. T. . Hausdorff dimension of sets arising in number theory. Number Theory, New York, 1983–84 (Lecture Notes in Mathematics, 1135). Springer, Berlin, 1985, pp.1–8.Google Scholar

[9] Cassels, J. . An Introduction to Diophantine Approximation. Cambridge University Press, New York, 1957.Google Scholar

[11] Falconer, K. J. . Fractal Geometry, Mathematical Foundations and Application. John Wiley & Sons, Chichester, 1990.Google Scholar

[13] Fan, A. H. and Feng, D. J. . On the distribution of long-term average on the symbolic space. J. Stat. Phys. 99(3) (2000), 813–856.CrossRefGoogle Scholar

[14] Fan, A. H. , Feng, D. J. and Wu, J. . Recurrence, dimension and entropy. J. London Math. Soc. 64(2) (2001), 229–244.CrossRefGoogle Scholar

[15] Good, I. J. . The fractional dimensional theory of continued fractions. Proc. Camb. Philos. Soc. 37 (1941), 199–228.CrossRefGoogle Scholar

[16] Hanus, P. , Mauldin, R. D. and Urbański, M. . Thermodynamic formalism and multifractal analysis of conformal infinite iterated function systems. Acta. Math. Hungar. 96(1–2) (2002), 27–98.CrossRefGoogle Scholar

[17] Hardy, G. and Wright, E. . An Introduction to the Theory of Numbers, 5th edn. Oxford University Press, New York, 1979.Google Scholar

[18] Hensley, D. . The Hausdorff dimensions of some continued fraction Cantor sets. J. Number Theory 33(2) (1989), 182–198.CrossRefGoogle Scholar

[19] Hensley, D. . A polynomial time algorithm for the Hausdorff dimension of continued fraction Cantor sets. J. Number Theory 58(1) (1996), 9–45.CrossRefGoogle Scholar

[20] Jarnik, I. . Zur metrischen Theorie der diophantischen Approximationen. Proc. Mat. Fyz. 36 (1928), 91–106.Google Scholar

[21] Jenkinson, O. and Pollicott, M. . Computing the dimension of dynamically defined sets: E ₂ and bounded continued fractions. Ergod. Th. & Dynam. Sys. 21(5) (2001), 1429–1445.CrossRefGoogle Scholar

[22] Jenkinson, O. . On the density of Hausdorff dimensions of bounded type continued fraction sets: the Texan conjecture. Stoch. Dyn. 4(1) (2004), 63–76.CrossRefGoogle Scholar

[23] Jenkinson, O. . Geometric barycentres of invariant measures for circle maps. Ergod. Th. & Dynam. Sys. 21(2) (2001), 511–532.CrossRefGoogle Scholar

[24] Kesseböhmer, M. and Stratmann, B. . A multifractal analysis for Stern–Brocot intervals, continued fractions and Diophantine growth rates. J. Reine Angew. Math. 605 (2007), 133–163.Google Scholar

[25] Khintchine, A. Ya. . Continued Fractions. University of Chicago Press, Chicago, London, 1964.Google Scholar

[26] Iosifescu, M. and Kraaikamp, C. . The Metrical Theory on Continued Fractions (Mathematics and its Applications, 547). Kluwer Academic, Dordrecht, 2002.CrossRefGoogle Scholar

[27] Mauldin, R. D. and Urbański, M. . Dimensions and measures in infinite iterated fuction systems. Proc. London Math. Soc. (3) 73(1) (1996), 105–154.CrossRefGoogle Scholar

[28] Mauldin, R. D. and Urbański, M. . Conformal iterated function systems with applications to the geometry of continued fractions. Trans. Amer. Math. Soc. 351(12) (1999), 4995–5025.CrossRefGoogle Scholar

[29] Mauldin, R. D. and Urbański, M. . Graph Directed Markov Systems – Geometry and Dynamics of Limit Sets Series (Cambridge Tracts in Mathematics, 148). Cambridge University Press, Cambridge, 2003.CrossRefGoogle Scholar

[30] Mayer, D. . A zeta function related to the continued fraction transformation. Bull. Soc. Math. France 104 (1976), 195–203.CrossRefGoogle Scholar

[31] Mayer, D. . Continued fractions and related transformations. Ergodic Theory, Symbolic Dynamics, and Hyperbolic Spaces (Trieste, 1989). Oxford Science Publications, Oxford University Press, New York, 1991, pp.175–222.Google Scholar

[32] Mayer, D. . On the thermodynamics formalism for the Gauss map. Comm. Math. Phys. 130 (1990), 311–333.CrossRefGoogle Scholar

[33] Pesin, Y. B. . Dimension Theory in Dynamical Systems: Contemporary Views and Applications (Chicago Lectures in Mathematics). University of Chicago Press, Chicago, 1998.Google Scholar

[34] Pollicott, M. and Weiss, H. . Multifractal analysis of Lyapunov exponent for continued fraction and Manneville–Pomeau transformations and applications to Diophantine approximation. Comm. Math. Phys. 207(1) (1999), 145–171.CrossRefGoogle Scholar

[35] Walters, P. . An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79). Springer, Berlin, 1982.CrossRefGoogle Scholar

[36] Walters, P. . Invariant measures and equilibrium states for some mappings which expand distances. Trans. Amer. Math. Soc. 236 (1978), 121–153.CrossRefGoogle Scholar

[37] Walters, P. . Convergence of the Ruelle operator for a function satisfying Bowen's condition. Trans. Amer. Math. Soc. 353(1) (2001), 327–347.CrossRefGoogle Scholar

[38] Walters, P. . A variational principle for the pressure of continuous transformations. Amer. J. Math. 97(4) (1975), 937–971.CrossRefGoogle Scholar

[39] Wu, J. . A remark on the growth of the denominators of convergents. Monatsh. Math. 147(3) (2006), 259–264.CrossRefGoogle Scholar

youngwheark.blogspot.com

Source: https://www.cambridge.org/core/services/aop-cambridge-core/content/view/4529304AC2E63EE35A9C0AA89E9D2F39/S0143385708000138a.pdf/on_khintchine_exponents_and_lyapunov_exponents_of_continued_fractions.pdf

Share this post